本コラムでは、これから許容応力度計算を始めたい方、力学に対する理解を深めたい方に向けて
専門的な知識をより分かりやすく解説し、業務に役立つ情報を提供できればと考えております。
メルマガを購読されているユーザー様へは、HP公開よりいち早くお届けしますのでぜひご登録ください!
●危険か?安全か?
第3回で「剛性とは」を荷重変形グラフや経験を例に考え、結果として以下を得ました。
・荷重変形グラフ上では傾きが剛性(モノのかたさとやわからさ)を意味し、傾きが大きいほどモノはかたい
・モノの剛性を定めるのは、材料だけではない(断面も剛性に影響している)
・剛性から断面の影響を排除するには基準化が有効な手段で、断面で基準化した力を応力度と呼んでいる
第3回で登場した「応力度」は、構造が関連する業務で頻繁に登場する言葉です。
なぜ、頻繁に登場するのでしょうか?
第3回ではフェア・アンフェアに感じるといった感覚的な表現で応力度を考えたこともあって、
応力度が頻繁に登場する理由がピンとこない方も少なくないかもしれません。
そこで、別の例で応力度が頻繁に登場する理由を考えてみましょう。
ある柱Aに10kN(約1トン)の力が作用しているとします。この柱Aは安全でしょうか(壊れないと言えるでしょうか)?

様々な答え方がありそうですが、「安全か否かはわからない」が答えのように思えます。
なぜ、安全か否かがわからないのでしょうか?
それは、ある柱Aの断面が割り箸のように小さければ壊れそうだし、軸組柱のような105mm角の断面であれば
安全のように思えるからではないでしょうか。
安全か?危険か?を考えるために、柱に具体的な断面をあたえてみましょう。
ある柱Aの断面を1cm角(割り箸ぐらいの断面)、ある柱Bの断面を10cm角(軸組柱ぐらいの断面)とします。
「割り箸のように小さければ壊れそう」や「軸組柱のような105mm角の断面であれば安全のように思える」を曖昧な言葉でなく、
具体的に表現するにはどうすればよいでしょうか。
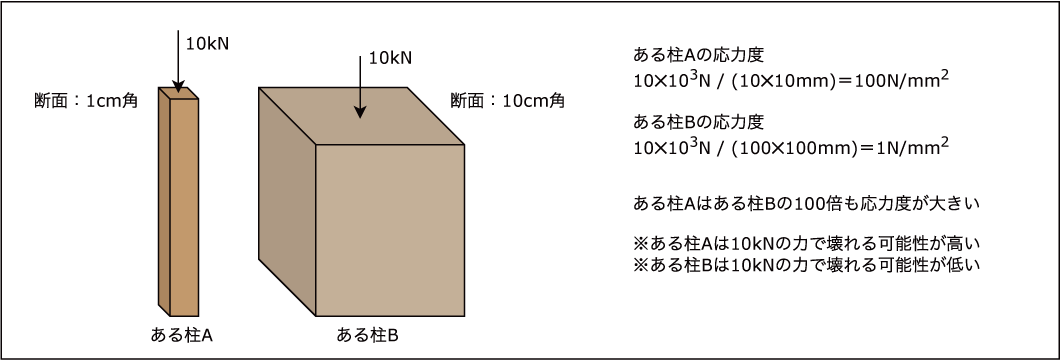
ここでも応力度が有効な表現方法であることに気付きます。
ある柱Aとある柱Bの応力度をそれぞれ計算すると、ある柱A(割り箸ぐらいの断面)は、ある柱B(軸組柱ぐらいの断面)の100倍も
応力度が大きいことがわかります。感覚的に考えた結果と計算結果がよく一致しています。
力の大きさだけ(10kNが作用しているという情報だけ)では安全か否かの判断はできませんでしたが、力を断面で基準化した
応力度であれば判断できました。これが構造で応力度が頻繁に登場する主な理由のひとつです。
応力度についてより深く理解できたので、つぎは第3回の最後に書いた
「実は材料そのもののかたさを知るには断面を基準化するだけでは不十分です」について考えてみましょう。
先に結論を言うと、モノの長さも剛性に影響します。
実際に輪ゴムを使って実験してみるとよりよくわかると思います。
下図の例は、長さだけが違う輪ゴムです(材料と断面と作用している力は輪ゴムAと輪ゴムBで同じです)。
※下図は輪ゴムを切って棒状にしたモノのイメージ図です
実験すると輪ゴムAの伸びが輪ゴムBの2倍伸びていることがわかります。
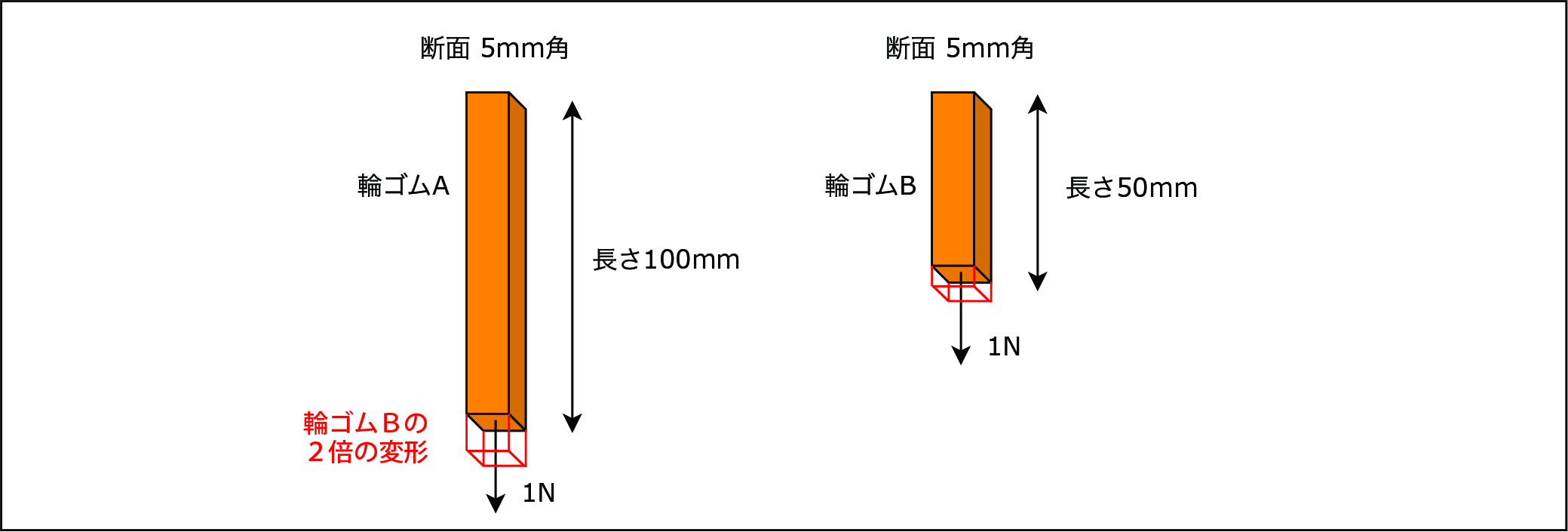
長さ以外の条件が同じなのに、伸びが倍違うということは、モノの長さがモノのかたさに影響していることを意味しています。
第3回のコラムのグラフで確認するとわかりやすいと思いますので以下に再掲します(グラフの表現を少し変更しています)。
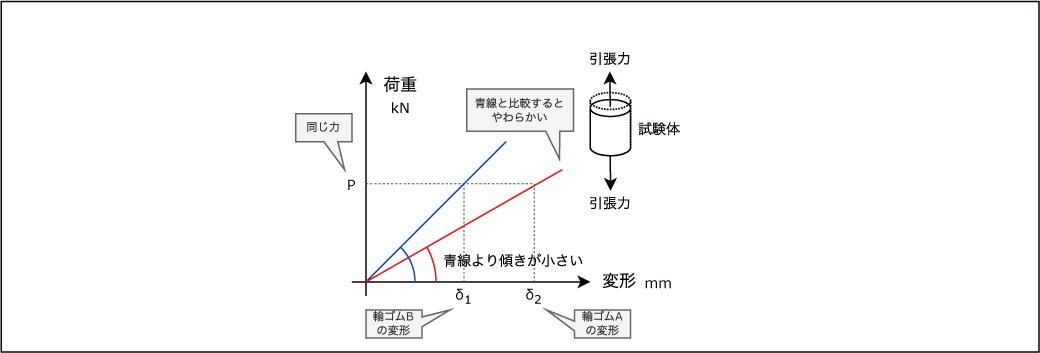
輪ゴムの実験を通してモノの長さがモノのかたさに影響することがわかりましたが、具体的に表現するにはどうすればよいでしょうか。
断面と同じく基準化してみましょう(伸びをモノの長さLで基準化します)。
輪ゴムAの伸び(変形)が4mmだったと仮定します。すると、実験結果から輪ゴムBの伸び(変形)はその半分の2mmだと言えます。
また、輪ゴムAの長さは100mmで輪ゴムBの長さは50mmです。
輪ゴムAの変形をモノの長さで基準化 : δA / LA = 4mm / 100mm = 0.04
輪ゴムBの変形をモノの長さで基準化 : δB / LB = 2mm / 50mm = 0.04
伸び(変形)をモノの長さで基準化すると、同じ値になりました。これは、モノの長さの影響を排除できたことを意味しています。
表現をかえると、輪ゴムA・輪ゴムBのいずれもそれぞれの長さの4%伸びたことを意味しているとも言えます。
伸び(変形)を長さで基準化することを構造力学ではひずみ度と呼んでいます(ギリシャ文字のイプシロンεで表されます)。
ここまで考えてきたことを思い出してみると、ふとあることに気付きます。
断面の影響を排除した応力度、長さの影響を排除したひずみ度で荷重変形グラフを描き直すと荷重変形グラフはどうなるでしょうか。
下図の右側が描き直したグラフです。
このグラフは、モノのかたさややわらかさに影響をあたえる断面と長さを排除していますので、このグラフの傾きは材料そのものの
かたさを表していることになります。
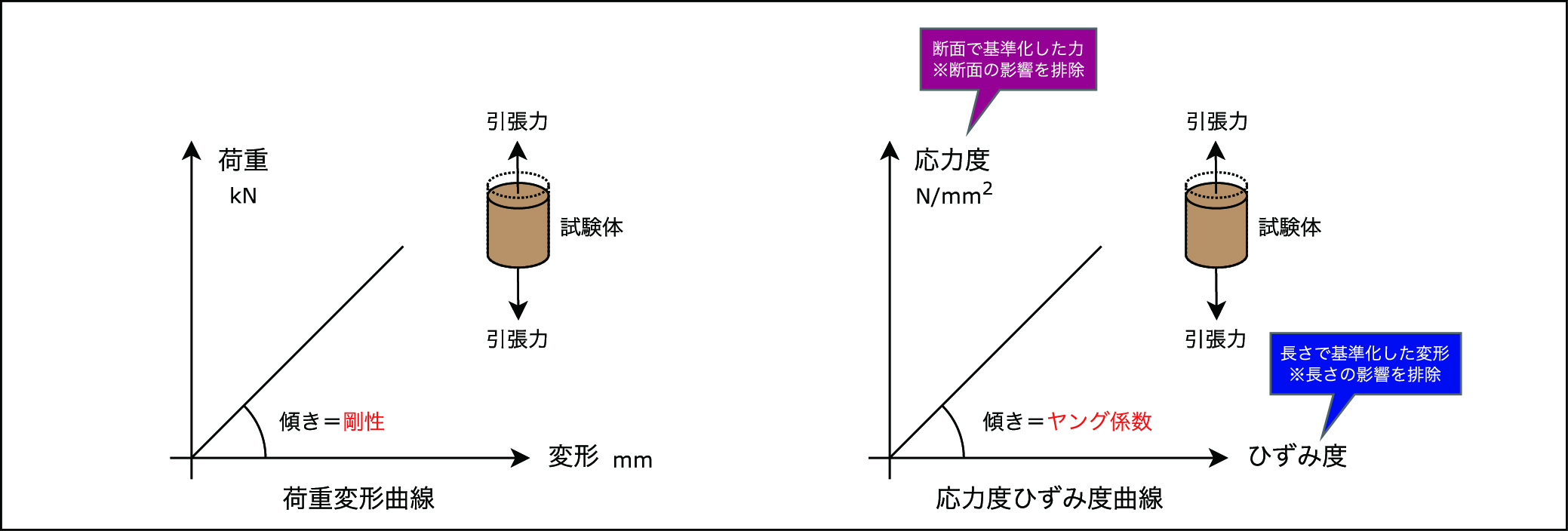
この傾きをヤング係数と呼んでいます(ヤング係数はEで表されます)。
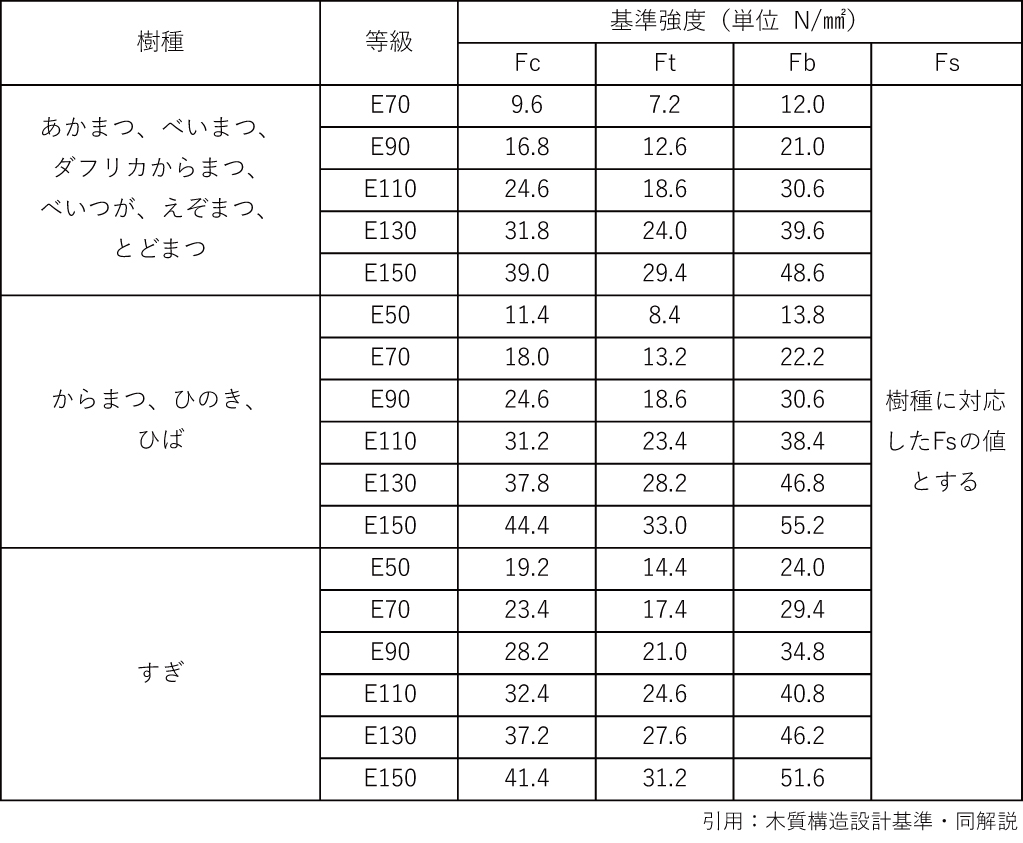
木材の強度等級を示すシール(例えば、E65-F225など)や建築基準法の材料強度の表などに記載されている値です。
また、このグラフを応力度ひずみ度曲線やSSカーブ(Stress-StrainCurve)などと呼んでいます。
 |  |